Palabras claves: material point method, simulación de impactos, simulación de explosiones, propagación de grietas, movimiento de material granular, descarga de silos, deslizamientos de tierra.
Debido a su independencia de las distorsiones de la malla, los métodos de partículas y los métodos sin malla presentan grandes ventajas sobre el tradicional método de elemento finito (MEF) en la simulación computacional de fenómenos de mecánica de sólidos que desarrollan grandes deformaciones y desplazamientos, ya sean estos estáticos o dinámicos. No obstante, muchos de los métodos de partículas y sin malla pagan un alto precio al momento del cálculo de la función de base para aproximación, debido principalmente al algoritmo de búsqueda de partículas o nodos vecinos dentro de una zona de influencia.
Sin embargo, existe un método de partícula llamado “material point method” (MPM) que combina lo mejor del método de elemento finito y los métodos de partículas logrando tremendas eficiencias computacionales. Las aplicaciones donde el MPM tiene un gran potencial para la simulación computacional del comportamiento mecánico de sólidos son todas aquellas donde hay movimiento de material particulado y separación/fragmentación de material. Algunos ejemplos incluyen: simulación de impactos, simulación de explosiones, propagación de grietas, movimiento de material granular, descarga de silos, deslizamientos de tierra, entre otros.
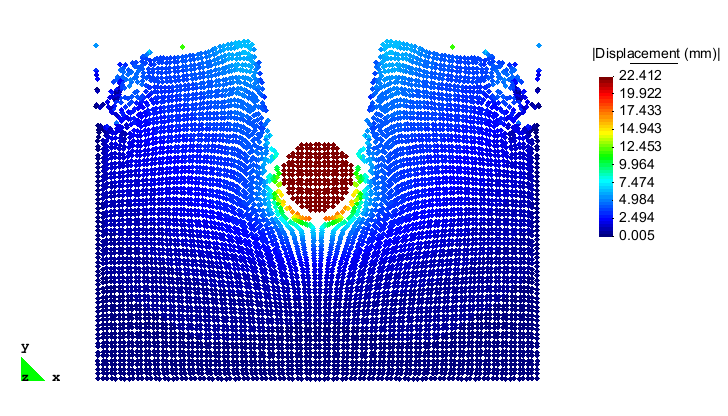
El siguiente video muestra la simulación del impacto de una bola de acero (muy rígida) a 1160 m/s sobre una placa de aluminio, con un tiempo de simulación de 50e-6 s. El problema fue resuelto de manera explícita en el tiempo (sin inversión de matrices) en un código programado en Matlab.
Prof. Alejandro Ortiz-Bernardin agradece al Prof. Vinh Phu Nguyen de Monash University por facilitar el código fuente original de MPM que fue utilizado como base para implementar este ejemplo numérico.